大概思路:
将图分为两部分,第一部分是已经加入最小生成树中的点,第二部分是未加入最小生成树的点,初始时,第一部分只有一个任选的顶点。在第二部分中找出距离第一部分中顶点最近的顶点以及对应的距离,将该顶点加入第一部分,依次类推,直到所有顶点都加入第一部分
算法步骤:
- 创建一个结构数组,数组的序号代表顶点的编号。数组元素包括每个未在最小生成树中的顶点离最小生成树中哪一个顶点(adindex)最近和相应的距离(closedge),若距离为零则该顶点已在最小生成树中。
- 初始时,任选一顶点V1放入最小生成树中,记录其余顶点到v1的距离lowcost(x表示不能一条边连通,无穷远)
- 找出数组中lowcost最小值及对应的顶点,将该顶点放入MST,该顶点的lowcost置为0
- 分别将lowcost不为0(不在MST中)的顶点v到最新加入MST的顶点的距离与 到与v的adjvex值对应的顶点的距离相比较,选出较小值及对应的顶点,更新lowcast
- 重复步骤2,3直到数组中所有的lowcost为0,即所有顶点均加入MST,最小生成树MST就此生成
图例说明:
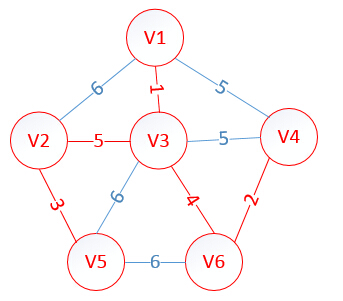
eg:对于原图:
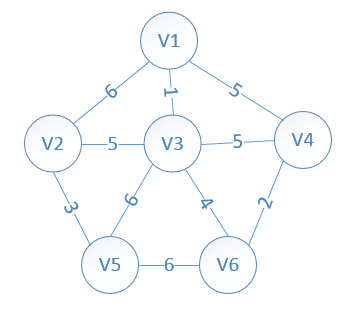
1.任选一顶点V1放入最小生成树中,记录其余顶点到v1的距离lowcost(x表示不能一条边连通,无穷远)
算法步骤:
- 创建一个结构数组,数组的序号代表顶点的编号。数组元素包括每个未在最小生成树中的顶点离最小生成树中哪一个顶点(adindex)最近和相应的距离(closedge),若距离为零则该顶点已在最小生成树中。
- 初始时,任选一顶点V1放入最小生成树中,记录其余顶点到v1的距离lowcost(x表示不能一条边连通,无穷远)
- 找出数组中lowcost最小值及对应的顶点,将该顶点放入MST,该顶点的lowcost置为0
- 分别将lowcost不为0(不在MST中)的顶点v到最新加入MST的顶点的距离与 到与v的adjvex值对应的顶点的距离相比较,选出较小值及对应的顶点,更新lowcast
- 重复步骤2,3直到数组中所有的lowcost为0,即所有顶点均加入MST,最小生成树MST就此生成
图例说明:
eg:对于原图:
1.任选一顶点V1放入最小生成树中,记录其余顶点到v1的距离lowcost(x表示不能一条边连通,无穷远)
| index | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| adjvex | 1 | 1 | 1 | 1 | 1 | 1 |
| lowcost | 0 | 6 | 1 | 5 | x | x |
2.找出lowcost最小值1及对应的顶点v3,将v3放入MST,v3的lowcost为0
| index | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| adjvex | 1 | 1 | 3 | 1 | 1 | 1 |
| lowcost | 0 | 6 | 0 | 5 | x | x |
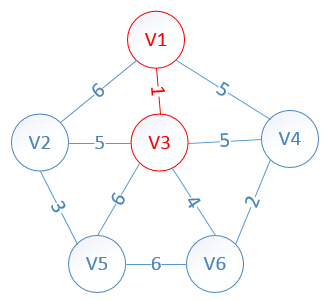
3.分别将lowcost不为0(不在MST中)的顶点到新加入MST的v3的距离与到与序号相对应的adjvex值的顶点距离相比较(eg:选序号顶点v2,序号2中adjvex为1,则将v2到v1的距离与v2到v3的距离相比较),选出较小值及对应的顶点,更新lowcast,eg:v2距离v1为6,距离v3为5,v2离v3更近,则将序号为2的元素中adjvex更新为3,lowcost更新为5,依此类推。
| index | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| adjvex | 1 | 3 | 1 | 3 | 3 | 3 |
| lowcost | 0 | 5 | 0 | 5 | 6 | 4 |
4.找出lowcast最小值为4,对应顶点v6,将v6放入MST中,v6的lowcast为0
| index | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| adjvex | 1 | 3 | 1 | 3 | 3 | 3 |
| lowcost | 0 | 5 | 0 | 5 | 6 | 0 |
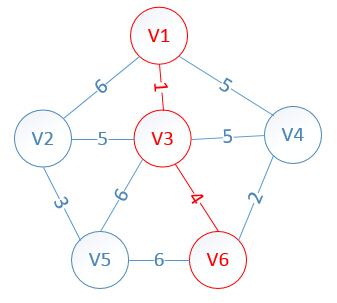
5.分别将lowcost不为0(不在MST中)的顶点到新加入MST的v3的距离与到上一加入MST的v1的距离相比较,选出较小值及对应的顶点,更新lowcast
| index | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| adjvex | 1 | 3 | 1 | 6 | 6 | 3 |
| lowcost | 0 | 5 | 0 | 2 | 6 | 0 |
6.找出lowcast最小值为2,对应顶点v4,将v4放入MST中,v4的lowcast为0
| index | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| adjvex | 1 | 3 | 1 | 6 | 6 | 3 |
| lowcost | 0 | 5 | 0 | 0 | 6 | 0 |
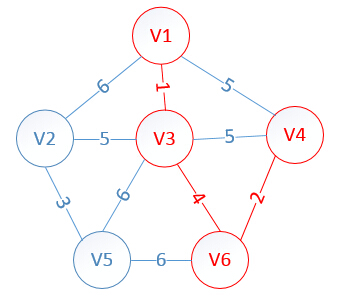
7.依次类推,最后得到的数组及最小生成树如下:
| index | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| adjvex | 1 | 3 | 1 | 6 | 2 | 3 |
| lowcost | 0 | 0 | 0 | 0 | 0 | 0 |
代码:
/**prime算法:从u号顶点出发构造最小生成树(MST)*/
void miniSpan(MGraph g, int u)
{
closedge[u].lowcost = 0; // S集(已经纳入生成树的点)初始仅有u顶点
// 其余顶点i距S集最近的邻接点是u顶点(初始仅有u顶点),距离即(u,i)的长度
for(int i=1; i<=g.vexnum; i++)
{
if(i!=u)
{
closedge[i].adjvex = u;
closedge[i].lowcost = g.matrix[u][i];
}
}
/**进行n-1次选择:将所有顶点逐个加入S集,对应最近边即为是MST的边,输出此边*/
for(int i=1; i<g.vexnum; i++)
{
/** 寻找closedge中lowcost最小,且 lowcost!=0(只考察在S集外的点)的顶点k
k号顶点即为S集外,距S集合中某点最近的点*/
int k;
for(k=1; closedge[k].lowcost == 0; k++) // 先找到第一个locaost不等于0的顶点k
;
for(int t=k+1; t<=g.vexnum; t++)
{
if(closedge[t].lowcost>0 && closedge[t].lowcost< closedge[k].lowcost)
{
k = t;
}
}
printf("%d --- %d\n", closedge[k].adjvex, k); // 输出一条边
closedge[k].lowcost = 0; // k号顶点加入S集合
/*因为k新加入S集合,需以此更新closedge:逐一考察各顶点是否与k顶点的边更近*/
for (int j=1; j<=g.vexnum; j++)
{
if(g.matrix[k][j] <closedge[j].lowcost) // j距离k点更短 则以此更新
{
closedge[j].adjvex = k;
closedge[j].lowcost = g.matrix[k][j];
}
}
}
}


