二叉树的基本操作

二叉树的基础了解

二叉树是n(n>=0)个结点的有限集合，该集合由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成,或者为空集（称为空二叉树。 由此可以看出二叉树根结点最多有两个子树，且分为左子树和右子树，左右子树顺序不可颠倒
如图：

二叉树的基础性质

• 在二叉树的第i层上最多有2^(i-1) 个节点 。（i>=1）
• 二叉树中如果深度为k,那么最多有2^k-1个节点。(k>=1）
• n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
• 若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对编号i:
  • 双亲结点编号：i/2 （i>1），若i=1则无双亲
  • 左孩子编号：2i（2i< n ) ,若2i>n 则无左孩子
  • 右孩子编号：2i+1（2i+1 < n）,若2i+1>n则无右孩子

满二叉树

    除了叶节点，其余结点的左支树和右子树不为空的二叉树

完全二叉树

    对一颗具有n个结点的二叉树按层编号，编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同的二叉树。

     二叉树是树中最基本也最重要的一种树结构，有必要好好总结一下关于二叉树的一些基本操作,主要是递归操作完成功能，因为二叉树的结构十分对称。

首先是包含头文件及一些准备工作

    #include <iostream>
    #include <fstream>
    #include <algorithm>
    #include <vector>
    
    using namespace std;
    typedef int T;
    
    typedef
    struct BiNode
    {
        T data;
        BiNode *lch;                // 指向左孩子，即左子树的根指针
        BiNode *rch;
    } *BiTree;
    
    ifstream fin("BitreeData.txt"); // 文件输入流,从文件BitreeData.txt读取数据建立二叉树
    

构建二叉树

    /*建立二叉树,若输入<=0则建立空树,返回树根指针*/
    BiTree  Create()
    {
        T e;
        fin >> e;        // 从文件(流)中输入一个元素值
        if( e<=0 )
            return 0;    // 返回空树
    
        BiTree t = new BiNode; // 生成根结点
        t->data = e;
    
        t->lch = Create();  // 递归建立t的左子树t->lch
        t->rch = Create();  // 递归建立t的右子树t->rch
    
        return t;
    }

遍历

       二叉树的遍历有三种:先序遍历（根 左子树 右子树），中序遍历（ 左子树 根 右子树） ，后续遍历（ 左子树 右子树 根）。先中后的顺序是按根节点的遍历顺序规定的。

/* 中序遍历--- 左子树 根 右子树*/

    void Travse(BiTree t)
    {
        if (0 == t)
            return;

        Travse(t->lch);            // 中序遍历t的左子树
        cout << t->data << "  ";   //访问根结点
        Travse(t->rch);            // 中序遍历t的右子树 
    }

只需调换Travse(t->lch); cout << t->data << "  ";  Travse(t->rch); 这三条语句的位置即可实现不同的遍历顺序

求树的结点数

1.直接返回t的结点数

    int  countNode(BiTree t)
    {
        if( 0 == t)  // 空树:0个结点
            return 0;
        return countNode(t->lch) + countNode(t->rch) +1; // t的结点数等于其左右子树之和+1(根节点)
    }

通过遍历求t的结点数

    /*注意n必须保留改变后的值，是引用参数*/
    void TravseCount(BiTree t, int &n)
    {
        if (0== t)
            return;
        ++n;       //根结点计数
        TravseCount(t->lch,n);
        TravseCount(t->rch,n);
    }

求二叉树的叶子数

    int countLeaves(BiTree h)
    {
        /* 注意有两个递归出口,且顺序不可交换*/
        if(0 == h)                 //空树返回0 
            return 0;
        if( 0 == h->lch && 0 == h->rch )   //只有根结点左右子树为空返回1 
            return 1;

        return countLeaves(h->lch) + countLeaves(h->rch);
    }

求二叉树的高度

    int height(BiTree t)
    {
        if( 0 == t)        //递归出口：空树返回 
            return 0;
        //二叉树高度为左右子树中较大高度者加一（根） 
        return max(height(t->lch),height(t->rch))+1;   //max函数包含在头文件<algorithem>中 
    }

查找

       查二叉树t，值为e的结点，查找成功返回其指针，否则返回0指针 若有重复元素，则返回最左的结点。

    BiNode* Locate(BiTree t, T e)
    {
        if( 0 == t)
            return 0;
        if(t->data == e)        //根找到值返回值对应节点的指针 
            return t;

        BiNode *p = Locate(t->lch,e);   //根没找到值，到左子树查找 
        if(p) 
            return p;                    //左子树找到值，返回值对应节点的指针 
        return Locate(t->rch,e);//左子树没找到值，到右子树查找，若找到返回值对应节点的指针，否则返回0指针 
    }

镜像二叉树

    void Mirror(BiTree &t)
    {
        if(0==t) //空树不用处理
            return;
        if(t->lch==0 && t->rch == 0) // 只有根结点，也不用处理
            return;
        swap(t->lch,t->rch);  // 交换根结点
        Mirror(t->lch);       // 左子树镜像
        Mirror(t->rch);       // 右子树镜像
    }

输出路径

       输出二叉树中p所指结点到指定值为e的子孙结点的路径，向量vec保存当前路径,此法会将整个二叉树遍历一遍，如果有多个值为e的元素，输出全部路径

    void dispPath(vector<BiNode*> vec)  //将结点指针存放在顺序表里，vector是动态存储可任意删添元素，十分方便 
    {
        for(int i=0; i<vec.size(); ++i)  //输出存放在vec里的结点指向的data，即输出路径 
        {
            cout << vec[i]->data <<" ";
        }
        cout << "\t\t";
    }

    void  FindPath(BiNode* p, T e, vector<BiNode*> vec) // vec不是引用,返回后其状态回溯
        {
            if(0 == p)
                return;
        
            vec.push_back(p);   // 当前结点追加到向量尾部
            if( e == p->data)   // 根找到值，当前结点即为终点，输出路径
            {
                dispPath(vec);
            }
            FindPath(p->lch, e, vec);   //根没找到值，p的左子树p->lch中 找路径
            FindPath(p->rch, e, vec);  // p的右子树p->lch中 找路径
        }

得到二叉树的副本

    /* 复制二叉树t，返回其副本*/
    BiTree copy(BiTree t)
    {
        if(0==t)
            return 0;

        BiNode *tt = new BiNode; //复制根结点
        tt->data = t->data;

        tt->lch = copy(t->lch); // 复制左子树
        tt->rch = copy(t->rch); // 复制右子树

        return tt;
    }

以前序序列和中序序列构造二叉树

       以前序序列pre[pl...pr]和中序序列mid[ml...mr]构造出二叉树，假定两序列合法。

思路

       由于前序序列先遍历根结点，故根结点在子树结点的前面，中序序列先遍历左子树结点后遍历根节点最后左子树节点，故根结点在左右子树结点中间。可通过前序序列找根结点，在中序序列找到前序序列找到的根结点，该根节点两边分别是左子树和右子树的结点左右子树结点，由此可以构造出一个二叉树。一个前序遍历和一个中序遍历可以确定一个唯一的二叉树.

eg：已知一颗二叉树的先序序列为EBADCFHG，其中序序列为ABCDEFGH。下图说明了还原二叉树的过程：

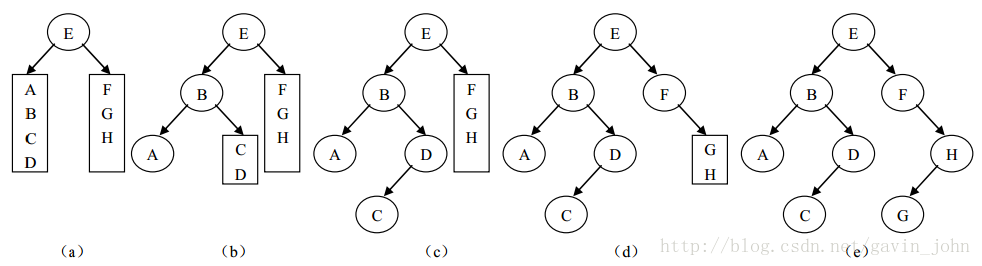
    首先由先序序列知道二叉树的根结点为E，在中序序列中找到E，则其左子树的中序序列为ABCD，左子树有四个结点，则在先序序列中根结点E的后面四个结点BADC就是左子树先序序列，以此类推。

    /*返回a[l...r]中值为e的下标*/
    int search(T a[],int l, int r,T e)
    {
        for (int i=l; i<=r; i++)
            if( a[i] == e)
                return i;

        return -1;
    }

    BiTree   Create(T pre[],int pl,int pr, T mid[], int ml,int mr)
    {
        BiNode *t;
        T e;
        if( pl > pr )  //  序列长度为0，返回空树
            return 0;

        e = pre[pl];   // 前序序列第一个元素就是根结点
        t = new BiNode;
        t->data = e;

        int k = search(mid,ml,mr,e);  // 在中序序列中 寻找根结点元素的位置
        int leftLen = k - ml;         // 左子树有leftLen个结点
        // pre[pl+1...pl+leftLen] 和 mid[ml,k-1]来建立左子树t->lch
        t->lch = Create(pre,pl+1,pl+leftLen, mid, ml,k-1);
        // 建立右子树t->rch
        t->rch = Create(pre,pl+leftLen+1, pr, mid , k+1,mr);

        return t;
    }

文件内容：

    1 2  4 0 0  5 6 0 0  0   3 0 7 0 0

    本序列 是前序方式建立二叉树的输入序列，0代表空(子)树
    请画出此二叉树，对照运行结果

一个有趣的实例：哈夫曼树和哈夫曼编码